Build A Info About How To Solve A Parallel Line

Unraveling the Mystery of Parallel Lines

1. What Exactly Are Parallel Lines?

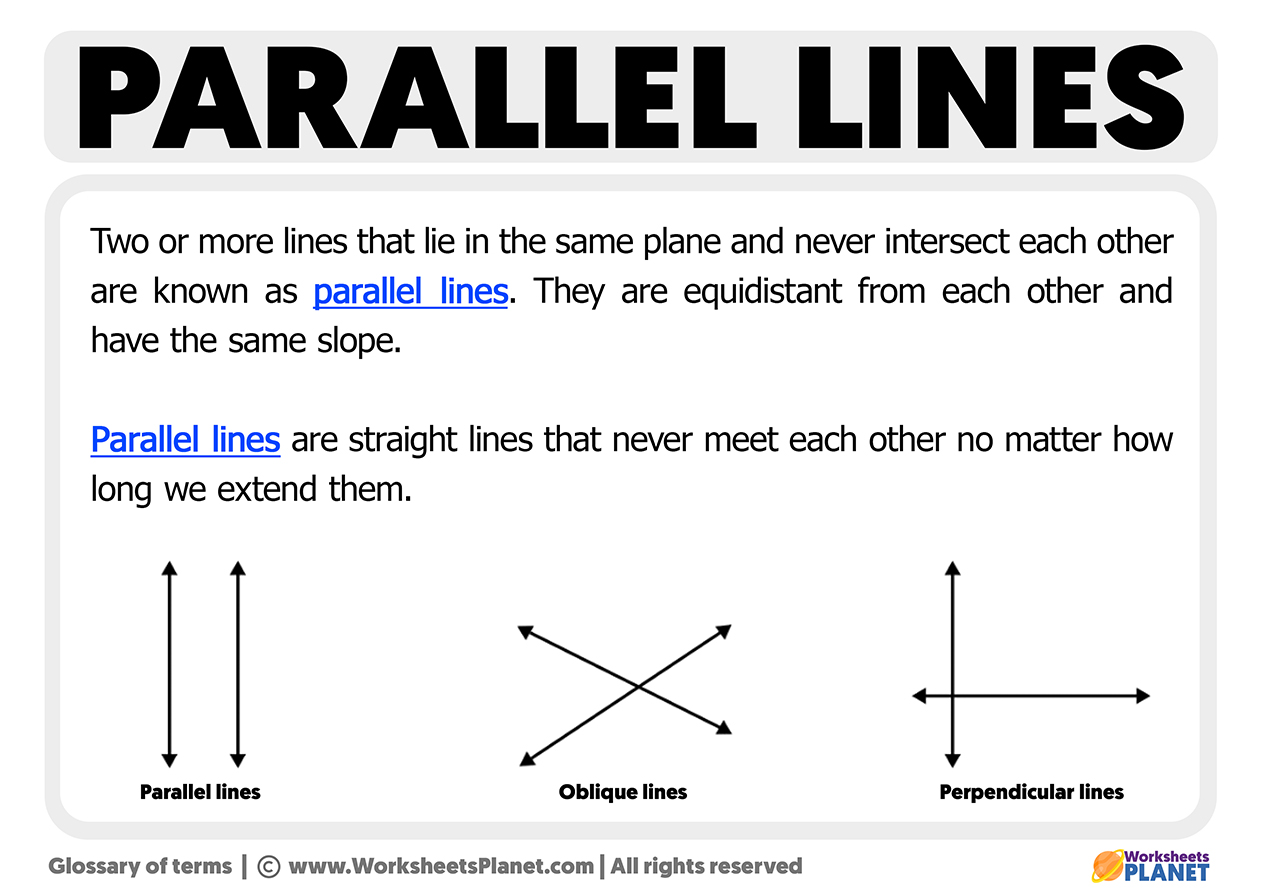
Alright, let's tackle this head-on. You know those train tracks that seem to go on forever without ever meeting? That's the basic idea behind parallel lines. In the world of geometry (which, let's be honest, can sometimes feel like another planet), parallel lines are lines that exist in the same plane and never, ever intersect. Think of them as shy lines, perpetually avoiding each other's company. No awkward collisions here!

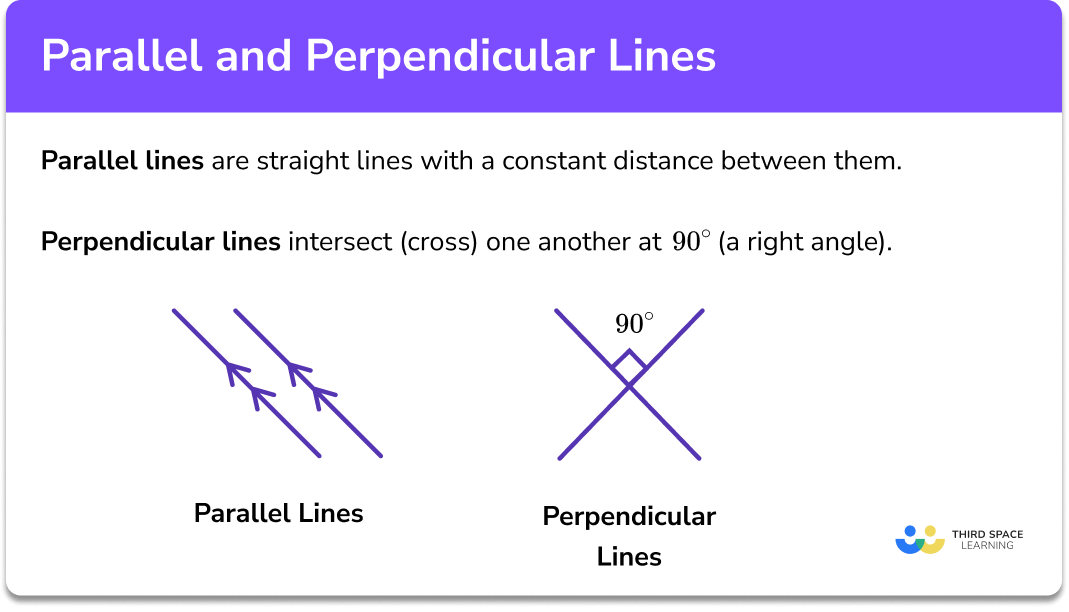
But it's not just about lines that look like they won't intersect. The key to them being parallel is that they maintain a constant distance from each other. It doesn't matter if you extend them to infinity (or as far as your ruler will allow); they'll never cross. It's a beautiful, mathematically enforced social distancing.

To make things even more interesting, parallel lines always have the same slope. Remember slope from algebra class? It's that whole "rise over run" thing. If two lines have the exact same rise over run, they're destined to be parallel. It's like they're singing the same tune, just on different parts of the paper.

So, in a nutshell, parallel lines are lines in the same plane that never intersect and have the same slope. They're the epitome of geometric harmony, living in perfect, non-intersecting bliss. Who knew math could be so poetic?

2. Spotting Parallel Lines in the Wild (and on Your Homework)

Now that we know what parallel lines are, how do we actually identify them? Well, keep your eyes peeled! You'll find them everywhere once you start looking. Picture the opposite sides of a perfectly rectangular book. Boom! Parallel. Or those lanes painted on the highway (hopefully, they're parallel for a smooth ride!).

In geometry problems, things get a little more formal. You might see little arrows pointing in the same direction on two lines. That's a visual cue that those lines are parallel. It's like the geometry gods are giving you a helpful wink. You might also encounter information about angles formed when another line (a transversal) crosses the two lines. Certain angle relationships (like corresponding angles being equal) are dead giveaways that the original lines are parallel.

Don't be fooled by appearances, though! Lines might look parallel but, without proof (like matching slopes or those special angle relationships), you can't assume they are. Always rely on the given information and the rules of geometry. Think of it like this: just because someone looks like a celebrity doesn't mean they actually are a celebrity. You need proof!

So, look for straight lines in the same plane, maintain a constant distance and having the same slope, pay attention to those handy arrows, and remember your angle relationships. With a little practice, you'll be spotting parallel lines like a geometry pro!

The Art of Proving Parallel Lines

3. Using Slope to Show Parallelism

Alright, time to get down to business. One of the most straightforward ways to prove that two lines are parallel is by demonstrating that they have the same slope. Remember the slope formula? (m = (y2 - y1) / (x2 - x1)) Dust it off, because it's about to become your best friend. If you're given two points on each line, you can calculate the slope of each line independently. If those slopes turn out to be identical — bingo! You've proven that the lines are parallel.

This method is particularly useful when you're working with coordinate geometry, where you have the coordinates of points readily available. It's a clean, algebraic approach that leaves no room for doubt. It's like presenting irrefutable evidence in a court of math.

But what if you don't have points on the lines, but instead have equations for the lines in slope-intercept form (y = mx + b)? Well, then it's even easier! Just identify the 'm' value in each equation — that's your slope! If the 'm' values are the same, congratulations, you've found parallel lines.

Just remember to properly show your work. Don't just state that the slopes are the same; demonstrate how you calculated them. Clear and well-documented calculations are the key to convincing anyone (especially your math teacher) that you know what you're talking about. It's all about the presentation!

4. Harnessing Angles Formed by Transversals

Things get even more interesting when a transversal enters the picture. A transversal is a line that intersects two or more other lines. When a transversal crosses two lines, it creates a whole bunch of angles — corresponding angles, alternate interior angles, alternate exterior angles, and same-side interior angles. And certain relationships between these angles can prove that the original lines are parallel.

For instance, if corresponding angles are congruent (meaning they have the same measure), then the lines are parallel. Think of corresponding angles as angles that occupy the same "corner" position at each intersection point. If those corners match up perfectly, it's a sign of parallelism.

Similarly, if alternate interior angles are congruent, the lines are parallel. Alternate interior angles are on opposite sides of the transversal and inside the two lines. And if same-side interior angles are supplementary (meaning they add up to 180 degrees), then — you guessed it — the lines are parallel. These angle relationships provide a powerful toolkit for proving parallelism, even when you don't have slope information.

But remember, the converse of these theorems must also be true. You can't assume lines are parallel just because some angles look like they might be congruent or supplementary. You need to verify the relationships meet the theorem's conditions to definitively conclude the two lines are parallel.

Practical Applications

5. Real-World Examples of Parallelism

Okay, so we've covered the theory, but where do parallel lines actually show up in the real world? Well, everywhere! Architecture is a prime example. Buildings often feature parallel lines in their design, whether it's the parallel edges of walls, windows, or even the lines formed by floor tiles. These parallel elements contribute to the overall stability and visual appeal of the structure.

In engineering, parallel lines are crucial for ensuring precision and accuracy. Think about the design of bridges or roads. Parallel lines are used to create consistent lanes and supports, contributing to the safety and functionality of these structures. The careful application of parallel lines helps ensure the structural integrity and efficient operation of countless engineering projects.

Even in everyday objects, you'll find parallel lines. The lines on a notebook, the edges of a ruler, and the strings on a guitar are just a few examples. These parallel lines help us organize information, measure accurately, and create harmonious sounds.

So, the next time you're walking around, take a moment to notice the parallel lines that surround you. They're a testament to the power and practicality of geometry in shaping our world.

6. Parallel Lines in Computer Graphics and Design

Parallel lines also play a significant role in the digital world. In computer graphics and design, parallel lines are used to create perspective, depth, and realistic representations of objects. Artists and designers use parallel lines to establish vanishing points and create the illusion of three-dimensional space on a two-dimensional screen.

In CAD (Computer-Aided Design) software, parallel lines are essential for creating accurate and precise technical drawings. Engineers and architects use CAD software to design everything from buildings and bridges to machine parts and electronic circuits. The ability to easily create and manipulate parallel lines is crucial for ensuring the accuracy and functionality of these designs.

Even in video games, parallel lines are used to create realistic environments and gameplay. Game developers use parallel lines to design roads, buildings, and other objects in the game world. The careful use of parallel lines helps create a sense of depth and realism that immerses players in the game.

From architectural renderings to video game environments, parallel lines are a fundamental tool for creating visually compelling and technically accurate digital representations of the world around us.